- El Método de Mapa Karnaugh.
Un mapa de Karnaugh (también conocido como tabla de Karnaugh o diagrama de Veitch, abreviado como Mapa-K o Mapa-KV) es un diagrama utilizado para la simplificación de funciones algebraicas Booleanas. El mapa de Karnaugh fue inventado en 1953 por Maurice Karnaugh, un físico y matemático de los laboratorios Bell.
Los mapas de Karnaugh reducen la necesidad de hacer cálculos extensos para la simplificación de expresiones booleanas, aprovechando la capacidad del cerebro humano para el reconocimiento de patrones y otras formas de expresión analítica, permitiendo así identificar y eliminar condiciones muy inmensas.
El mapa de Karnaugh consiste en una representación bidimensional de la tabla de verdad de la función a simplificar. Puesto que la tabla de verdad de una función de N variables posee 2N filas, el mapa K correspondiente debe poseer también 2N cuadrados. Las variables de la expresión son ordenadas en función de su peso y siguiendo el código Gray, de manera que sólo una de las variables varía entre celdas adyacentes. La transferencia de los términos de la tabla de verdad al mapa de Karnaugh se realiza de forma directa, albergando un 0 ó un 1, dependiendo del valor que toma la función en cada fila. Las tablas de Karnaugh se pueden fácilmente realizar a mano con funciones de hasta 6 variables, para funciones de mayor cantidad de variables es más eficiente el uso de software especializado.
Al calcular el numero de renglones y columnas debemos tomar en cuenta:
Normalmente suele representarse como un mapa cuadrado (número de renglones = número de columnas) cuando el número de variables es par (2, 4, 6, 8... etc) y cuando el número de variables es impar el número de renglones igual a la mitad del número de columnas; siguiendo la siguientes fórmulas:
Cuando el número de variables es par:

Cuando el número de variables es impar:


Ejemplo:
Dada la siguiente función algebraica booleana representada como el sumatorio de sus minitérminos, y con las variables Booleanas A, B, C, D, la función se puede representar con dos notaciones distintas:


Tabla de Verdad
Las variables de entrada pueden combinarse de 16 formas diferentes, por lo que el mapa de Karnaugh tendrá 16 celdas, distribuidas en una cuadrícula de 4 × 4. La razón por la cual en las tablas de 4 variables (por ejemplo) hay una transición de una columna rotulada como "01" a otra "11" (en vez de "10" que sería el próximo valor binario) se debe a que es un requisito en la construcción del mapa que en cada nueva columna (de izquierda a derecha) sólo varíe una variable a la vez. Entonces, al "01" le sigue el "11", de tal forma que sólo varía el primer bit, cosa que no ocurriría si se pasará del "01" al "10" (porque cambiarían ambos bits a la vez).
- El Método Algebraico.
Para la simplificación por este método no sólo bastará con conocer todas las propiedades y teoremas del álgebra de Boole, además se debe desarrollar una cierta habilidad lógico-matemática que se adquiere fundamentalmente con la experiencia.
Como ejemplo se simplificará la siguiente función:
F = A’C’ + ABC + BC’ + A’B’C + A’BC
Observando cada uno de los sumando podemos ver que hay factores comunes en los sumandos 2º con 5º y 4º con 5º que conllevan simplificación:
F = A’C’ + BC’ + BC(A + A’) + A’C(B + B’)
Note que el término 5º se ha tomado dos veces, de acuerdo con la propiedad que dice que A + A = A. Aplicando las propiedades del álgebra de Boole (A + A' = 1 y A . 1 = A), queda
F = A’C’ + BC’ + BC + A’C
Repitiendo nuevamente el proceso,
F = A’( C’ + C) + B( C’ + C) = A’ + B
No siempre las funciones son tan fáciles de simplificar como la anterior. El método algebraico, por lo general, no resulta cómodo para los no expertos, a los cuales, una vez simplificada una ecuación le pueden quedar serias dudas de haber conseguido la máxima simplificación.
Numérico de Quine-McCluskey
El algoritmo Quine-McCluskey permite la simplificación de funciones lógicas de cualquier número de variables y es el que se utiliza para diseñar aplicaciones informáticas en las que se necesite obtener funciones simplificadas.
A continuación se indican los pasos a seguir en este método a partir de un ejemplo.
Se expresa la función a simplificar en su forma canónica de suma de productos.
Sea la siguiente función a simplificar:

Se forma una tabla con el valor decimal de la combinación, el estado de las variables y el índice (número de unos que contiene el estado de las variables).
Se agrupan las combinaciones cuyos estados difieren en una sola variable, sustituyéndola por un guion bajo (_). Las combinaciones utilizadas se marcan con un aspa (X). Hay que fijarse en las combinaciones cuya diferencia entre sus respectivos índices es la unidad.
Se repite el proceso anterior las veces que sean necesarias y se van eliminando estados idénticos.
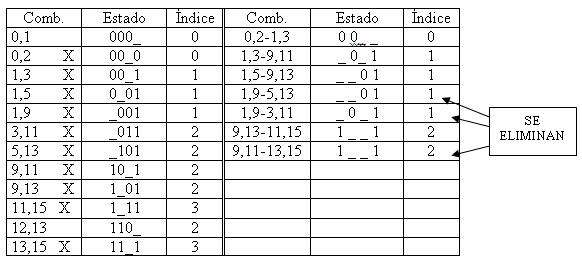
Se forma una tabla con las combinaciones finales y las no agrupadas. Se toman como filas las combinaciones finales y las no agrupadas y como columnas los valores decimales de dichas combinaciones. Cada celda que contenga el valor decimal de una combinación se marca con un aspa. A continuación nos fijamos en aquellas columnas con una sola aspa; sus combinaciones serán esenciales. Finalmente se toman aquellas combinaciones de los valores decimales no seleccionados, teniendo precaución de no tomar aquellas combinaciones cuyos valores decimales hayan sido ya tomados en otras combinaciones. La función simplificada final viene dada por las combinaciones esenciales y estas últimas.
Un mapa de Karnaugh (también conocido como tabla de Karnaugh o diagrama de Veitch, abreviado como Mapa-K o Mapa-KV) es un diagrama utilizado para la simplificación de funciones algebraicas Booleanas. El mapa de Karnaugh fue inventado en 1953 por Maurice Karnaugh, un físico y matemático de los laboratorios Bell.
Los mapas de Karnaugh reducen la necesidad de hacer cálculos extensos para la simplificación de expresiones booleanas, aprovechando la capacidad del cerebro humano para el reconocimiento de patrones y otras formas de expresión analítica, permitiendo así identificar y eliminar condiciones muy inmensas.
El mapa de Karnaugh consiste en una representación bidimensional de la tabla de verdad de la función a simplificar. Puesto que la tabla de verdad de una función de N variables posee 2N filas, el mapa K correspondiente debe poseer también 2N cuadrados. Las variables de la expresión son ordenadas en función de su peso y siguiendo el código Gray, de manera que sólo una de las variables varía entre celdas adyacentes. La transferencia de los términos de la tabla de verdad al mapa de Karnaugh se realiza de forma directa, albergando un 0 ó un 1, dependiendo del valor que toma la función en cada fila. Las tablas de Karnaugh se pueden fácilmente realizar a mano con funciones de hasta 6 variables, para funciones de mayor cantidad de variables es más eficiente el uso de software especializado.





- El Método Algebraico.
Para la simplificación por este método no sólo bastará con conocer todas las propiedades y teoremas del álgebra de Boole, además se debe desarrollar una cierta habilidad lógico-matemática que se adquiere fundamentalmente con la experiencia.
Como ejemplo se simplificará la siguiente función:
F = A’C’ + ABC + BC’ + A’B’C + A’BC
Observando cada uno de los sumando podemos ver que hay factores comunes en los sumandos 2º con 5º y 4º con 5º que conllevan simplificación:
F = A’C’ + BC’ + BC(A + A’) + A’C(B + B’)
Note que el término 5º se ha tomado dos veces, de acuerdo con la propiedad que dice que A + A = A. Aplicando las propiedades del álgebra de Boole (A + A' = 1 y A . 1 = A), queda
F = A’C’ + BC’ + BC + A’C
Repitiendo nuevamente el proceso,
F = A’( C’ + C) + B( C’ + C) = A’ + B
No siempre las funciones son tan fáciles de simplificar como la anterior. El método algebraico, por lo general, no resulta cómodo para los no expertos, a los cuales, una vez simplificada una ecuación le pueden quedar serias dudas de haber conseguido la máxima simplificación.
Numérico de Quine-McCluskey
El algoritmo Quine-McCluskey permite la simplificación de funciones lógicas de cualquier número de variables y es el que se utiliza para diseñar aplicaciones informáticas en las que se necesite obtener funciones simplificadas.
A continuación se indican los pasos a seguir en este método a partir de un ejemplo.
Se expresa la función a simplificar en su forma canónica de suma de productos.
Sea la siguiente función a simplificar:

Se forma una tabla con el valor decimal de la combinación, el estado de las variables y el índice (número de unos que contiene el estado de las variables).
Se agrupan las combinaciones cuyos estados difieren en una sola variable, sustituyéndola por un guion bajo (_). Las combinaciones utilizadas se marcan con un aspa (X). Hay que fijarse en las combinaciones cuya diferencia entre sus respectivos índices es la unidad.
Se repite el proceso anterior las veces que sean necesarias y se van eliminando estados idénticos.

Se forma una tabla con las combinaciones finales y las no agrupadas. Se toman como filas las combinaciones finales y las no agrupadas y como columnas los valores decimales de dichas combinaciones. Cada celda que contenga el valor decimal de una combinación se marca con un aspa. A continuación nos fijamos en aquellas columnas con una sola aspa; sus combinaciones serán esenciales. Finalmente se toman aquellas combinaciones de los valores decimales no seleccionados, teniendo precaución de no tomar aquellas combinaciones cuyos valores decimales hayan sido ya tomados en otras combinaciones. La función simplificada final viene dada por las combinaciones esenciales y estas últimas.
Para la simplificación por este método no sólo bastará con conocer todas las propiedades y teoremas del álgebra de Boole, además se debe desarrollar una cierta habilidad lógico-matemática que se adquiere fundamentalmente con la experiencia.
Como ejemplo se simplificará la siguiente función:
F = A’C’ + ABC + BC’ + A’B’C + A’BC
Observando cada uno de los sumando podemos ver que hay factores comunes en los sumandos 2º con 5º y 4º con 5º que conllevan simplificación:
F = A’C’ + BC’ + BC(A + A’) + A’C(B + B’)
Note que el término 5º se ha tomado dos veces, de acuerdo con la propiedad que dice que A + A = A. Aplicando las propiedades del álgebra de Boole (A + A' = 1 y A . 1 = A), queda
F = A’C’ + BC’ + BC + A’C
Repitiendo nuevamente el proceso,
F = A’( C’ + C) + B( C’ + C) = A’ + B
No siempre las funciones son tan fáciles de simplificar como la anterior. El método algebraico, por lo general, no resulta cómodo para los no expertos, a los cuales, una vez simplificada una ecuación le pueden quedar serias dudas de haber conseguido la máxima simplificación.
Numérico de Quine-McCluskey
El algoritmo Quine-McCluskey permite la simplificación de funciones lógicas de cualquier número de variables y es el que se utiliza para diseñar aplicaciones informáticas en las que se necesite obtener funciones simplificadas.
A continuación se indican los pasos a seguir en este método a partir de un ejemplo.
Se expresa la función a simplificar en su forma canónica de suma de productos.
Sea la siguiente función a simplificar:
Se forma una tabla con el valor decimal de la combinación, el estado de las variables y el índice (número de unos que contiene el estado de las variables).
Se agrupan las combinaciones cuyos estados difieren en una sola variable, sustituyéndola por un guion bajo (_). Las combinaciones utilizadas se marcan con un aspa (X). Hay que fijarse en las combinaciones cuya diferencia entre sus respectivos índices es la unidad.
Se repite el proceso anterior las veces que sean necesarias y se van eliminando estados idénticos.
Se forma una tabla con las combinaciones finales y las no agrupadas. Se toman como filas las combinaciones finales y las no agrupadas y como columnas los valores decimales de dichas combinaciones. Cada celda que contenga el valor decimal de una combinación se marca con un aspa. A continuación nos fijamos en aquellas columnas con una sola aspa; sus combinaciones serán esenciales. Finalmente se toman aquellas combinaciones de los valores decimales no seleccionados, teniendo precaución de no tomar aquellas combinaciones cuyos valores decimales hayan sido ya tomados en otras combinaciones. La función simplificada final viene dada por las combinaciones esenciales y estas últimas.





No hay comentarios.:
Publicar un comentario